4.1　变换三维对象

本章的主要目标是对三维对象（如茶壶）进行改变，以创建在视觉上有所不同的新三维对象。在第2章中，平移或缩放构成二维恐龙的每个向量，整个恐龙形状也会相应地移动或改变大小。这里采取同样的方法。我们看到的每一种变换都以一个向量作为输入，并返回一个向量作为输出，如下面的伪代码所示。

def transform(v):
    old_x, old_y, old_z = v
    # 此处做一些计算
    return (new_x, new_y, new_z)

我们首先把熟悉的平移和缩放示例从二维改成三维的。

4.1.1　绘制变换后的对象

在初始化附录C中描述的依赖关系后，第4章源代码中的文件draw_teapot.py即可运行（参见附录A中关于从命令行运行Python脚本的说明）。如果运行成功，就可以看到如图4-4所示的PyGame窗口。

图4-4　运行draw_teapot.py的结果

接下来的几个示例会修改构成茶壶的向量，然后重新渲染，以查看几何效果。作为第一个示例，我们可以用相同的系数缩放所有向量。下面的函数scale2将一个输入向量乘以标量2.0并返回结果。

from vectors import scale
def scale2(v):
    return scale(2.0, v)

scale2(v)函数与本节开头给出的transform(v)函数形式相同：当传递一个三维向量作为输入时，scale2返回一个新的三维向量作为输出。对茶壶整体执行此变换需要变换每个顶点。对于用来构建茶壶的每个三角形，先将scale2应用到每个原始顶点，再用结果创建新的三角形。

original_triangles = load_triangles()      ←---- 使用附录C 中的代码加载三角形
scaled_triangles = [
    [scale2(vertex) for vertex in triangle]      ←---- 将scale2应用于给定三角形的每个顶点来获得新顶点
    for triangle in original_triangles      ←---- 对原始三角形列表中的每个三角形执行同样的操作
]

有了新的一组三角形，调用draw_model(scaled_triangles)就可以绘制它们。图4-5显示了执行调用后的茶壶，运行源代码中的scale_teapot.py文件即可重现。

图4-5　将scale2应用于每个三角形的每个顶点，可得到一个2倍大的茶壶

因为每个向量被乘以2，所以这个茶壶看起来比原来的大，准确地说是原来的2倍大。让我们对每个向量应用另一种变换：通过向量(-1, 0, 0)进行平移。

回想一下，“通过向量平移”是“加上这个向量”的另一种说法，其实就是为茶壶的每个顶点加上(-1, 0, 0)。这将使整个茶壶向轴负方向移动1个单位，从我们的角度看是向左移动。下面这个函数完成了对单个顶点的变换。

from vectors import add
def translate1left(v):
    return add((-1,0,0), v)

从原始三角形开始，现在要像以前一样缩放它们的每个顶点，然后应用平移。图4-6显示了结果。运行源文件scale_translate_teapot.py可重现这一过程。

scaled_translated_triangles = [
    [translate1left(scale2(vertex)) for vertex in triangle]
    for triangle in original_triangles
]
draw_model(scaled_translated_triangles)

图4-6　茶壶变大了并且按预期移动到了左边

不同的标量乘积会以不同的系数（标量倍数）改变茶壶的大小，而不同的平移向量会将茶壶移动到空间中的不同位置。在接下来的练习中，你将有机会尝试不同的标量乘积和平移向量，但现在，让我们专注于组合并应用更多的变换。

4.1.2　组合向量变换

依次应用任意数量的变换可以定义新的变换。例如，上一节中的缩放和平移可以变换茶壶，我们将这个新变换打包成自己的Python函数。

def scale2_then_translate1left(v):
    return translate1left(scale2(v))

这个原则很重要！因为向量变换以向量为输入和输出，所以可以通过函数组合来组合任意多的向量，即通过按照指定顺序应用两个或更多现有函数来定义新的函数。如果把函数scale2和translate1left想象成接收三维模型并输出新模型的机器（见图4-7），那么将第一台机器的输出作为第二台机器的输入可把它们组合起来。

图4-7　对茶壶先调用scale2，然后调用translate1left来输出转换后的版本

我们可以想象，将第一台机器的输出槽与第二台机器的输入槽焊接起来，可以隐藏中间步骤（见图4-8）。

图4-8　将两台函数机器焊接在一起，得到一台新的机器，从而一步完成两种转换

可以将结果看作一台新机器一步完成了原来两个函数的工作。这种函数的“焊接”也可以在代码中完成。我们可以实现一个通用的compose函数，接收两个Python函数（比如用于向量变换），然后返回一个新的函数，也就是它们的组合。

def compose(f1,f2):
    def new_function(input):
        return f1(f2(input))
    return new_function

我们不直接定义scale2_then_translate1left函数，而是像下面这样写。

scale2_then_translate1left = compose(translate1left, scale2)

你可能听说过这样一种思想：Python把函数当作“一等对象”。这句话的意思是：Python函数可以被赋给变量并作为输入传递给其他函数，或者被即时创建并作为输出值返回。这些都是函数式编程技术，也就是说，函数式编程可以通过组合现有函数来创建新函数，进而构建复杂的程序。

关于函数式编程在Python中是否合法（或者像Python爱好者所说的那样，函数式编程是否符合Python风格）存在一些争论。本章不会就编码风格发表意见，但是之所以使用函数式编程，是因为函数（即向量变换）是本章研究的核心。在介绍了compose函数之后，本章还会展示一些函数式编程的示例，让我们的这次“跑题”看起来更有价值。你可以在本书提供的源代码文件transforms.py中找到每一个示例。

接下来，我们会反复地取一种向量变换，并把它应用到定义一个三维模型的每个三角形的每个顶点上。为此，可以实现一个可复用的函数，而不是每次都实现新的列表推导式。下面的polygon_map函数接收一个向量变换和一个多边形（通常是三角形）列表，并将变换应用于每个多边形的每个顶点，产生一个新的多边形列表。

def polygon_map(transformation, polygons):
    return [
        [transformation(vertex) for vertex in triangle]
        for triangle in polygons
    ]

有了这个辅助函数，即可用一行代码把scale2应用到原来的茶壶上。

draw_model(polygon_map(scale2, load_triangles()))

函数compose和polygon_map都将向量变换作为参数，但有时候也需要将向量变换作为函数的返回值。例如，前面叫作scale2的函数在实现里硬编码了数2，我们也可以定义一个叫作scale_by的函数，并返回一个缩放向量的函数。

def scale_by(scalar):
    def new_function(v):
        return scale(scalar, v)
    return new_function

有了这个函数，就可以通过scale_by(2)得到一个与scale2行为完全一样的函数。如图4-9所示，如果把函数当作有输入槽和输出槽的机器，那么可以把scale_by当作输入槽接收数并在输出槽输出新的函数机器。

图4-9　将数作为输入并产生新函数机器作为输出的函数机器

作为练习，你可以写一个类似的translate_by函数，将平移向量作为输入，并返回平移函数作为输出。在函数式编程的术语中，这个过程被称为柯里化（currying）。柯里化将接收多个输入的函数重构为返回另一个函数的函数。

这样做的结果是，得到一个行为相同但调用方式不同的程序机器。例如，对于任意输入和，scale_by(s)(v)的结果与scale(s,v)的结果相同。优点是，scale(...)和add(...)接收不同类型的参数，由此产生的函数scale_by(s)和translate_by(w)是可以互换的。接下来，本书将以类似的方式思考旋转问题：对于给定的任意角度，生成一个使模型以该角度旋转的向量变换。

4.1.3　绕轴旋转对象

第2章已经演示了如何旋转二维对象：将笛卡儿坐标转换为极坐标，按旋转系数增加或减少角度，然后再转换回来。尽管这是二维的技巧，但也适用于三维，因为从某种意义上说，所有的三维向量旋转在平面上都是孤立的。例如，试想三维点绕轴旋转，其坐标和坐标会改变，但坐标不变。如果一个给定的点绕轴旋转，无论旋转角度如何，其坐标都不会改变，该点保持在一个圆内（见图4-10）。

图4-10　绕轴旋转一个点

这意味着保持坐标不变，只对坐标和坐标应用二维旋转函数，可以使三维点围绕轴旋转。这里会浏览一遍代码，源代码中的rotate_teapot.py文件中有其实现。首先，根据第2章中的策略实现一个二维旋转函数。

def rotate2d(angle, vector):
    l,a = to_polar(vector)
    return to_cartesian((l, a+angle))

该函数接收一个角度和一个二维向量，并返回一个旋转的二维向量。现在，实现一个rotate_z函数，只对三维向量的坐标和坐标应用该函数。

def rotate_z(angle, vector):
    x,y,z = vector
    new_x, new_y = rotate2d(angle, (x,y))
    return new_x, new_y, z

继续用函数式编程范式思考并柯里化这个函数。给定任意角度，柯里化版的函数产生一个做相应旋转的向量变换。

def rotate![z](http://private.codecogs.com/gif.latex?z)by(angle):
    def new_function(v):
        return rotate_z(angle,v)
    return new_function

接着看一下实际情况，下面这行代码生成了图4-11中旋转角度为π/4弧度或45°的茶壶。

draw_model(polygon_map(rotate![z](http://private.codecogs.com/gif.latex?z)by(pi/4.), load_triangles()))

图4-11　茶壶绕轴逆时针旋转45°

可以实现一个类似的函数使茶壶绕轴旋转，这意味着旋转只影响向量的分量和分量。

def rotate_x(angle, vector):
    x,y,z = vector
    new_y, new_z = rotate2d(angle, (y,z))
    return x, new_y, new_z
def rotate_x_by(angle):
    def new_function(v):
        return rotate_x(angle,v)
    return new_function

在函数rotate_x_by中，固定坐标并在平面上执行二维旋转可以实现绕轴的旋转。下面的代码进行了一次绕轴90°或π/2弧度的逆时针旋转，结果是如图4-12所示的茶壶俯视图。

draw_model(polygon_map(rotate_x_by(pi/2.), load_triangles()))

图4-12　茶壶绕轴旋转π/2弧度

源文件rotate_teapot_x.py可用来重现图4-12。旋转后，茶壶的阴影是一致的。最亮的多边形在图的右上角，这在预料之中，因为光源在(1, 2, 3)。这是一个很好的迹象，表明我们成功地移动了茶壶，而不是像之前那样只改变了我们的OpenGL视角。

事实证明，通过在和方向上的旋转组合，可以完成任意想要的旋转。在4.1.5节的练习中，你可以尝试更多的旋转，但现在我们将继续学习其他类型的向量变换。

4.1.4　创造属于你自己的几何变换

让我们跳出前面章节提及的向量变换，看一下能否想出其他有趣的变换方法。需要记住，三维向量变换的唯一要求是，接收一个单独的三维向量作为输入，并返回一个新的三维向量作为输出。下面来看一些不属于我们所见任何类别的变换。

对于我们的茶壶，每次修改一个坐标。这个函数只在方向上将向量拉伸为原来的4倍（硬编码）。

def stretch_x(vector):
    x,y,z = vector
    return (4.*x, y, z)

结果是一个沿轴（壶嘴和把手所在的方向）拉伸的细长茶壶（见图4-13）。stretch_teapot.py完整地实现了这个变换。

图4-13　一个沿轴拉伸的茶壶

类似的stretch_y函数可以将茶壶上下拉伸。你可以自行实现stretch_y并将其应用于茶壶，应该得到图4-14中的图像。否则，可以参考源代码中stretch_teapot_y.py的实现。

图4-14　将茶壶沿方向拉伸

还可以发挥创意，通过坐标的三次方而不是简单地乘以一个数来拉伸茶壶。就像cube_teapot.py实现的那样，这种变换使茶壶的盖子被不成比例地拉长了，如图4-15所示。

def cube_stretch_z(vector):
    x,y,z = vector
    return (x, y*y*y, z)

图4-15　将茶壶的垂直尺寸按三次方拉伸

如果在变换公式中选择性地将三个坐标中的两个相加，如将坐标和坐标相加，茶壶会倾斜。这在slant_teapot.py中进行了实现，如图4-16所示。

def slant_xy(vector):
    x,y,z = vector
    return (x+y, y, z)

图4-16　为现有的坐标加上坐标，使茶壶向方向倾斜

我们的重点并不是判断哪一种变换最重要或最有用，对构成一个三维模型的所有向量进行任意数学变换，都会使模型的外观产生几何上的影响。这些变换可能导致模型变得太过扭曲以至于无法辨认，甚至无法成功绘制。确实，一些向量变换有更好的表现，我们将在下一节中对它们进行分类。

4.1.5　练习

练习4.1：实现一个translate_by函数（4.1.2节中有所提及），以一个平移向量作为输入并返回一个平移函数作为输出。

解：

def translate_by(translation):
    def new_function(v):
        return add(translation,v)
    return new_function

 

练习4.2：渲染沿轴负方向平移了20个单位的茶壶，产生的图像是什么样的？

解：可以用polgyon_map通过对每个多边形中的向量应用translate_by((0,0,-20))来实现。

draw_model(polygon_map(translate_by((0,0,-20)), load_triangles()))

请记住，我们是从轴上方5个单位看茶壶的。这个变换使茶壶离我们远了20个单位，所以它看起来小了很多（见图4-17）。源代码translate_teapot_down_z.py中有完整的实现。

图4-17　茶壶沿轴向下平移了20个单位。因为它离我们更远，所以显得更小

 

练习4.3（小项目）：当按0和1之间的标量缩放每一个向量时，茶壶会发生什么变化？按系数-1缩放，又会发生什么变化？

解：可以应用scale_by(0.5)和scale_by(-1)来查看结果（见图4-18）。

draw_model(polygon_map(scale_by(0.5), load_triangles()))
draw_model(polygon_map(scale_by(-1), load_triangles()))

图4-18　从左到右分别是原茶壶以及按系数0.5和-1缩放的茶壶

如图4-19所示，scale_by(0.5)将茶壶缩小到原来大小的一半。scale_by(-1)似乎将茶壶旋转了180°，但情况更复杂。它实际上把茶壶里外对调了！每个三角形都变成了原来的镜像，所以每个法向量现在都指向茶壶里而不是茶壶外。

图4-19　镜像操作会改变三角形的方向。左侧三角形的顶点按逆时针排列，而右侧镜像的顶点按顺时针排列。它们的法向量指向相反的方向

旋转茶壶，可以看到结果渲染得不太正确（见图4-20）。我们应该谨慎地对图形进行镜像操作！

图4-20　旋转后的镜像茶壶看起来很怪，其中一些关键特征发生了反转，比如在右下角的那一帧里，可以同时看到盖子和中空的底部

 

练习4.4：对茶壶首先应用translate1left，然后应用scale2。结果与相反的组合顺序有什么不同？为什么会这样？

解：将这两个函数按照指定的顺序组合，然后通过polygon_map应用它们。

draw_model(polygon_map(compose(scale2, translate1left), load_triangles()))

结果是，茶壶仍然是原来的2倍大。但如图4-21所示，右图中的茶壶比左图中的平移了更远的距离。这是因为在平移后应用了一个系数为2的缩放，平移的距离也翻倍了。你可以运行源文件scale_translate_teapot.py和translate_scale_teapot.py比较结果，验证我们的判断。

图4-21　对比缩放后平移的茶壶（左）和平移后缩放的茶壶（右）

 

练习4.5：compose(scale_by(0.4), scale_by(1.5))变换的效果是什么？

解：把一个向量依次按系数1.5和0.4进行缩放，净缩放系数为0.6。得到的图像将是原始大小的60%。

 

练习4.6：将compose(f,g)函数修改为compose(*args)，它将几个函数作为参数，并返回一个新的函数，即它们的组合。

解：

def compose(*args):
    def new_function(input):      ←---- 开始定义compose返回的函数
        state = input      ←---- 设置当前的state等于input
        for f in reversed(args):      ←---- 因为组合函数的内部函数先被执行，所以逆序迭代输入函数。例如，compose(f,g,h)(x)应该等于f(g(h(x)))，所以第一个应用的函数是h
            state = f(state)      ←---- 在每一步，通过执行下一个函数更新state。最终的state 使得所有的函数以正确的顺序执行
        return state
    return new_function

为了检查上述工作，我们可以实现一些函数，并将它们组合起来。

def prepend(string):
    def new_function(input):
        return string + input
    return new_function

f = compose(prepend("P"), prepend("y"), prepend("t"))

然后运行f("hon")返回字符串"Python"。函数f会将字符串"Pyt"附加到任何给定的字符串上。

 

练习4.7：实现函数curry2(f)，接收一个有两个参数的Python函数f(x,y)，并返回一个柯里化版本。例如，对于g = curry2(f)，f(x,y)和g(x)(y)应该返回相同的结果。

解：返回值应该是一个新函数，而这个新函数在被调用时又会产生一个新函数。

def curry2(f):
    def g(x):
        def new_function(y):
            return f(x,y)
        return new_function
    return g

举个例子，scale_by函数可以这样实现。

>>> scale_by = curry2(scale)
>>> scale_by(2)((1,2,3))

(2, 4, 6)

 

练习4.8：在不执行代码的情况下，说出变换compose(rotate_z_by(pi/2),rotate_x_by(pi/2))的结果是什么。如果换一下组合的顺序呢？

解：这个组合相当于绕轴顺时针旋转π/2弧度。颠倒顺序，则是绕轴逆时针旋转π/2弧度。

 

练习4.9：实现函数stretch_x(scalar,vector)，只在方向上将目标向量按给定系数缩放。同时实现stretch_x_by的柯里化版本，使stretch_x_by(scalar)(vector)返回同样的结果。

解：

def stretch_x(scalar,vector):
    x,y,z = vector
    return (scalar*x, y, z)

def stretch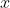![x](http://private.codecogs.com/gif.latex?x)by(scalar):
    def new_function(vector):
        return stretch_x(scalar,vector)
    return new_function